【VR課堂 3D優課】高中數學必修2 《空間直角坐標系》

【教學目標】

重點: 空間直角坐標系，空間中點的坐標及空間坐標對應的點.

難點：右手直角坐標系的理解，空間中的點與坐標的一一對應。

知識點：空間直角坐標系的相關概念，空間中點的坐標以及空間坐標對應的點.

能力點：理解空間直角坐標系的建立過程，以及空間中的點與坐標的一一對應.

教育點：通過空間直角坐標系的建立，體會由二維空間到三維空間的拓展和推廣，讓學生建立發展的觀點；通過空間點與坐標的對應關系，進一步加強學生對“數形結合”思想方法的認識.

自主探究點：如何由空間中點的坐標確定點的位置。

考試點：空間中點的確定及坐標表示.

教具準備  多媒體課件和VR/3D互動教學課件

課堂模式  學案導學、分組討論

【教學過程】

一、引入新課

由數軸上的點和平面直角坐標系內的點的表示引入空間中點的表示。數軸Ox上的點M,可用與它對應的實數x表示；直角坐標平面內的點M可以用一對有序實數（x,y）表示。類似于數軸和平面直角坐標系（一維坐標系和二維坐標系），當我們建立空間直角坐標系（三維坐標系）后，空間中任意一點可用有序實數組（x,y,z）表示。

二、探究新知

（一）空間直角坐標系及相關概念

如圖所示，OABC-D'A'B'C' 是單位正方體.以O為原點，分別以射線QA、OC、OD'的長為單位長，建立三條數軸：x軸、y軸、z軸。這時我們說建立了一個空間直角坐標系Oxyz，其中O點叫做坐標原點，x軸、y軸、z軸叫做坐標軸。通過每兩個坐標軸的平面叫做坐標平面，分別稱為xoy平面、yoz平面、zox平面。

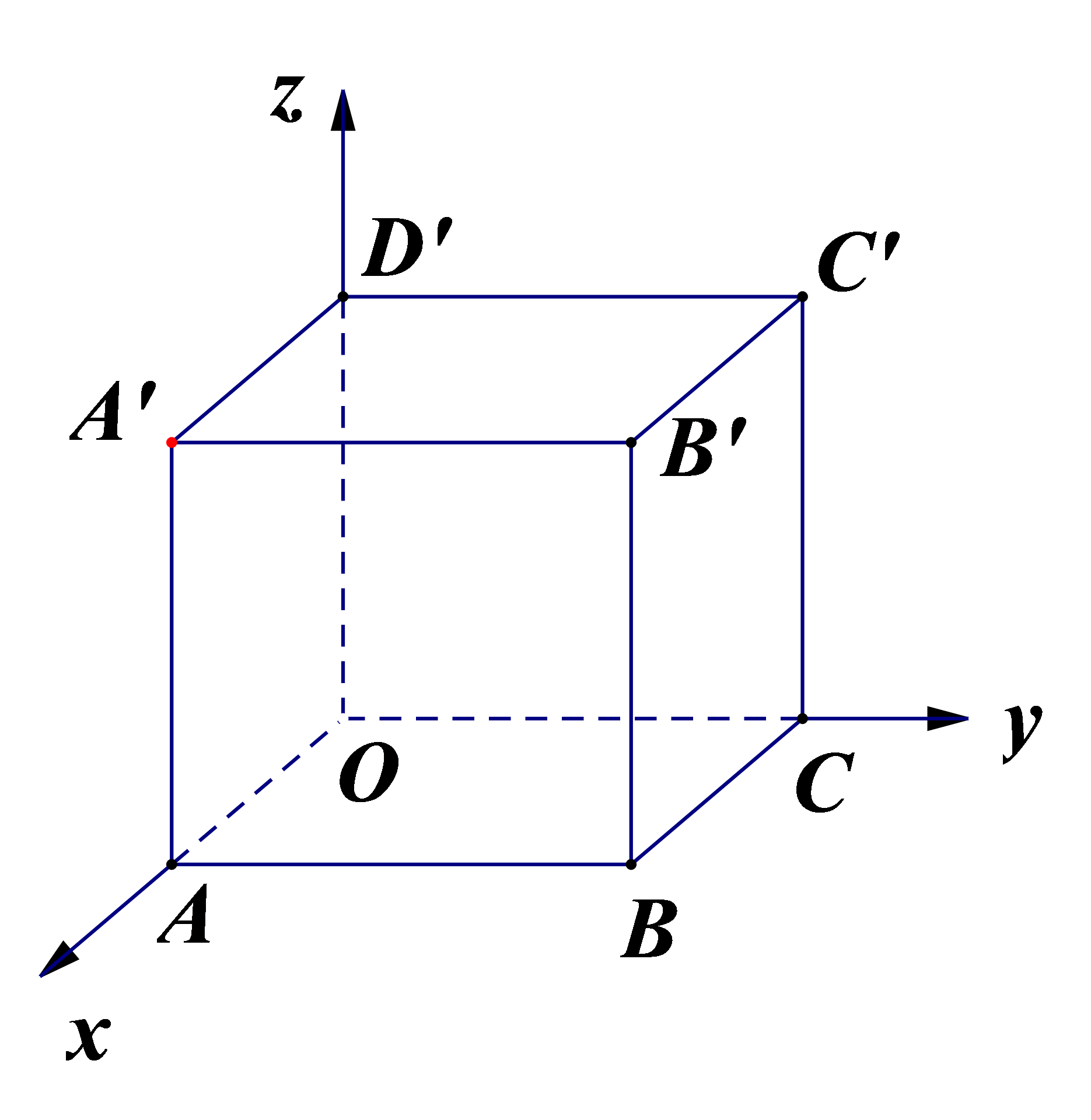
【師生活動】由空間直角坐標系的定義，結合正方體直觀圖的畫法，總結在平面上畫空間直角坐標系需要注意的問題：

1、空間直角坐標系的三要素：原點、坐標軸方向、單位長。

2、在平面上畫空間直角坐標系Oxyz時，一般使∠xOz=135°，∠yOz=90°。

3、在y軸、z軸上的長度都取原來的長度，而x在軸上的長度取原來長度的一半，即x軸上的單位長度在平面內表現出來時是y軸、z軸上的單位長度的一半。【設計意圖】加強學生對空間直角坐標系的認識，避免坐標軸上的單位長度選取不當造成的圖形直觀性差。

（二）右手直角坐標系

在空間直角坐標系中，讓右手拇指指向x軸的正方向，食指指向y軸的正方向，如果中指指向z軸的正方形，則稱這個坐標系為右手直角坐標系。

【引申拓展】右手直角坐標系的其它解釋方法：先把大拇指指向z軸正方向，把其余四指指向x軸正方向，然后握成拳頭，這時四指掃過原平面直角坐標系的第一象限從x軸正方向到軸正方向。

【設計意圖】上面補充的右手直角坐標系的其它解釋方法，與物理中的右手定則聯系起來，動態的解釋，使學生更容易理解什么是右手直角坐標系。

（三）空間中點的坐標以及空間中坐標表示的點

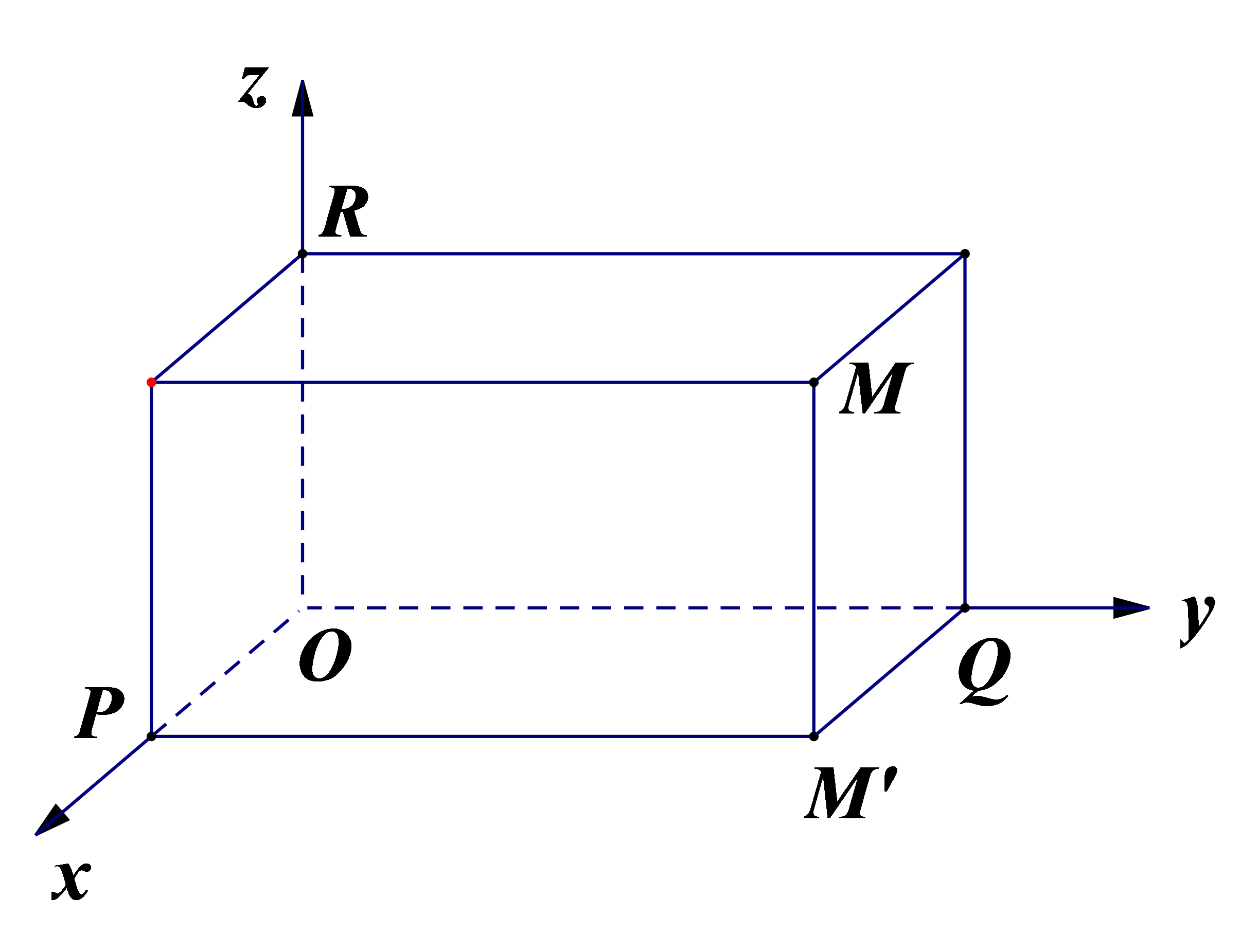
如圖所示，設M為空間的一個定點，過點M分別作垂直于x軸、y軸和z軸的平面，依次交x軸、y軸和z軸于點P、Q和R，設點P、Q和R在x軸、y軸和z軸上的坐標分別為x、y、z，那么點M就對應唯一確定的有序實數組（x,y,z）.反過來，給定有序實數組（x,y,z），我們可以在x軸、y軸和z軸上分別取坐標為實數x、y和z的點P、Q和R，分別過P、Q和R各作一個平面，分別垂直于x軸、y軸和z軸，這三個平面的唯一交點就是有序實數組（x,y,z）確定的點M。這樣，空間一點M的坐標可以用有序實數組（x,y,z）來表示，有序實數組（x,y,z）叫做點M在此空間直角坐標系中的坐標，記作M（x,y,z）.其中x叫做點M的橫坐標，y叫做點M的縱坐標，z叫做點M的豎坐標。

播放VR/3D互動教學系統視頻部分：三維空間內的坐標平面。視頻主要內容為：

1.了解空間直角坐標系，在已知空間內用x坐標、y坐標、z坐標來確定一個點。

2.了解直角坐標系的八大卦限。

【師生活動】

1.師：任意給定空間中的一點M，它的坐標是不是唯一確定的？生：是。

2.師：任意給定空間中的一個有序實數組（x,y,z），它所表示的點是不是唯一確定的？生：是.

【設計意圖】通過VR/3D互動教學系統互動部分的展示，讓學生認識到空間直角坐標系中的點與坐標的一一對應.

三、運用新知

     環節一：打開VR/3D互動教學系統部分：三維空間內的坐標平面——評估，點擊測試，以小組比賽形式回答系統的題目，每組10題，得分最高的小組獲勝。

【設計意圖】此環節除進一步加深學生對空間直角坐標系的認識和培養學生的空間想象能力外，還可以讓學生初步體會空間中點所在位置對應的卦限名稱。以小組比賽形式可激發學生的積極性，活躍課堂氣氛。

環節二： 結晶體的基本單位稱為晶胞，如圖是食鹽晶胞的示意圖(可看成是八個棱長為1/2的小正方體堆積成的正方體)，其中色點（淺色點）代表鈉原子，黑點（深色點）代表氯原子.如圖，建立空間直角坐標系O-xyz后，試寫出全部鈉原子所在位置的坐標。

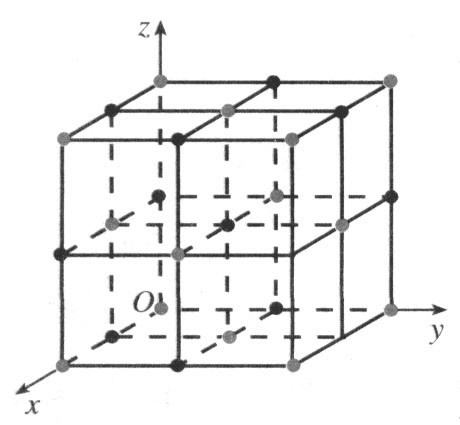
解：把圖中的鈉原子分成下、中、上三層來寫它們所在位置的坐標.

下層的原子全部在xoy平面上，它們所在位置的豎坐標全是0，所以這五個鈉原子所在位置的坐標分別是（0，0，0），（1,0,0），（1,1,0），（0,1,0），（1/2，1/2，0）

中層的原子所在的平面平行于xoy平面，與z軸交點的豎坐標為1/2，所以，這四個鈉原子所在位置的坐標分別是（1/2，0，1/2），（1，1/2,1/2），（1/2,1,1/2），（0，1/2，1/2）

上層的原子所在的平面平行于xoy平面，與z軸交點的豎坐標為，所以，這五個鈉原子所在位置的坐標分別是（0,0,1），（1,0,1），（1,1,1），（0,1,1），（1/2，1/2,1）

思考：如圖，棱長為a的正方體OABC-D’A’B’C’中，對角線OB’與BD’相交于點Q。頂點O為坐標原點，OA，OC分別在x軸、y軸的正半軸上。試寫出點Q的坐標。

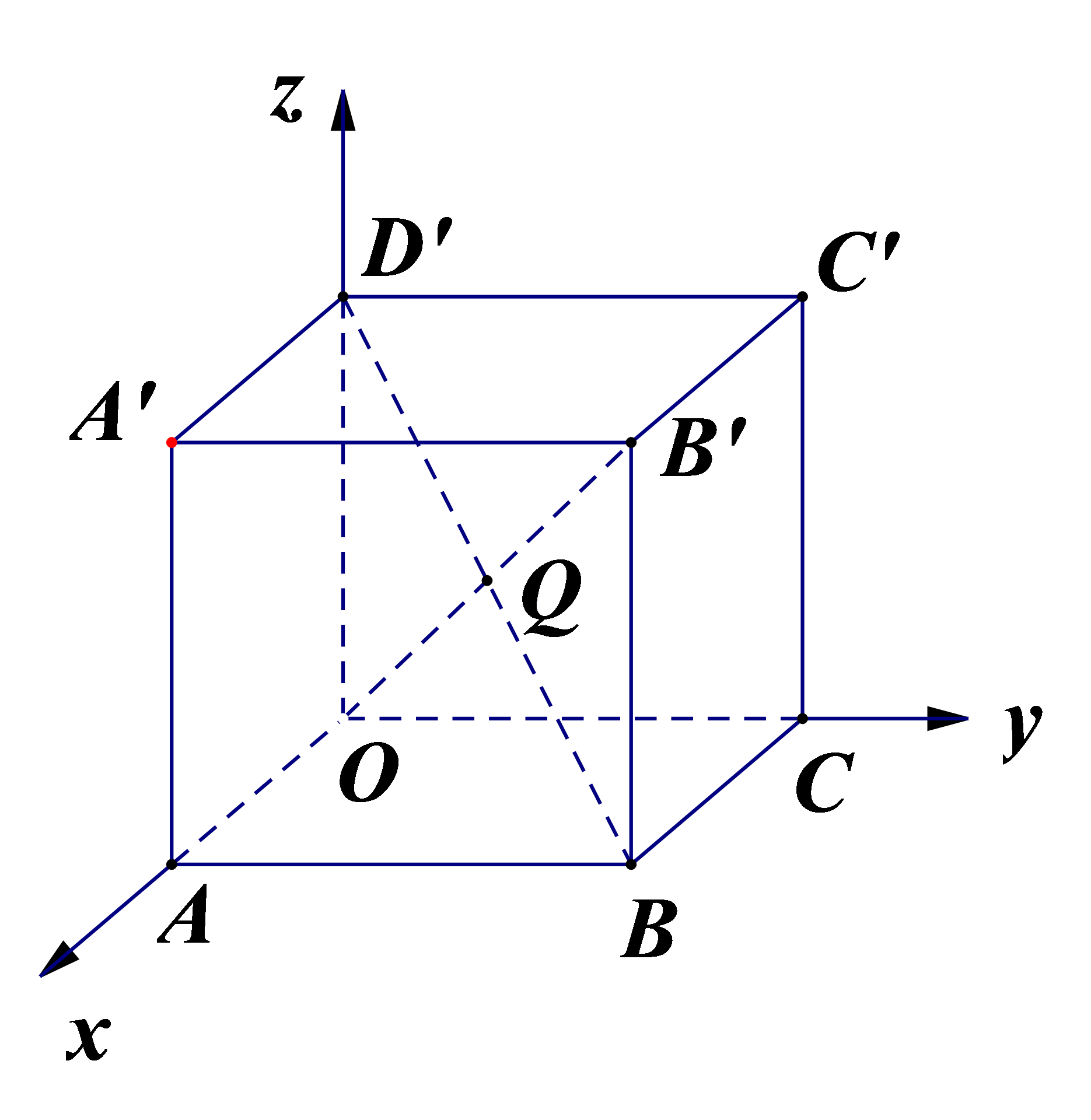
答案：Q（a/2，a/2，a/2）

【延伸拓展】空間中線段的中點坐標公式：在空間直角坐標系中，點P₁（x₁，y₁，z₁）點P₂（x₂，y₂，z₂）則線段P₁P₂的中點M的坐標為（(x₁+x₂)/2，(y₁+y₂)/2，(z₁+z₂)/2）。。

四、課堂小結 

本節課的知識：（提問學生歸納，老師適當點撥）

１。空間直角坐標系及相關概念。

２。空間直角坐標系中點的坐標及相關概念。

３。給出具體的點寫出它在空間直角坐標系中的坐標。

４。由具體的點的坐標找出它在空間直角坐標系中的位置。

五、布置作業  

1。閱讀教材P136—137，預習4.3.2空間兩點間的距離公式。

2.書面作業 ：課本P136  練習1。